Bem Vindo ao Mathemathikando.
(O blog encontra-se em permanente atualização).
A Matemática tem um notável potencial de revelação de estruturas e padrões que nos permitem compreender o mundo que nos rodeia.
Quando esses padrões são descobertos, ou inventados, muitas vezes em áreas científicas e tecnológicas aparentemente muito distintas, a Matemática pode ser usada para explicar, medir e controlar processos naturais. A Matemática tem uma influência universal no nosso quotidiano e contribui de forma decisiva para o progresso e bem-estar da humanidade.
Para além da sua beleza intrínseca e do seu conteúdo abstrato (axiomas, teoremas, teorias) a Matemática estimula diversos modos de pensamento, ao mesmo tempo versáteis e potentes, incluindo modelação, simulação, abstração, optimização, análise lógica e dedutiva, inferência a partir de dados, manipulação de símbolos e experimentação. Tem um campo de aplicações praticamente ilimitado, presente em quase todas as áreas do conhecimento humano.
A Matemática não impõe limites à imaginação. É a única ciência com a capacidade de passar das observações das coisas visíveis à imaginação das coisas invisíveis.
Estudar Matemática desenvolve múltiplas capacidades, competências e talento, essenciais a uma integração consistente e bem sucedida no atual mercado de trabalho.
Desenvolve o raciocínio lógico e dedutivo e as capacidades de generalização e abstração
Permite a modelação de situações reais e, através do seu potencial de representação simbólica (fórmulas, equações, gráficos), facilita a sua simulação, medição e controlo
Desenvolve a capacidade de formular e resolver problemas de forma precisa, conduzindo rapidamente ao cálculo, controlo, decisão e resulltados
Desenvolve a criatividade, a versatilidade de adaptação a novas situações e superação de novos desafios
Desenvolve a capacidade de sonhar! Permite imaginar mundos diferentes, e dá também a possibilidade de comunicar esses sonhos de forma clara e não ambígua.
Por tudo isto, ser matemático é enveredar por uma carreira profissional muitíssimo atraente, com um enorme potencial de realização pessoal. Para além das vias de ensino e de investigação pura e aplicada, as formações em Matemática abrem um campo vasto de oportunidades de carreiras profissionais, cada vez mais solicitadas pelas várias entidades empregadoras - empresas, serviços, indústria, finança, seguradoras, etc.

Então temos: c²= a²+b²
| a) Uma escola tem 25 professores, dos quais 24% ensinam Matemática. Quantos professores ensinam Matemática nessa escola? d) Na compra de um aparelho obtive desconto de 15% por ter feito o pagamento à vista. Se paguei R$ 102,00 reais pelo aparelho, qual era seu o preço original? Calcule as porcentagens correspondentes: e) 2% de 700 laranjas f) 40% de 48 m g) 38% de 200 Kg h) 6% de 50 telhas i) 37,6% de 200 j) 22,5% de 60 |
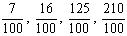

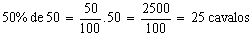
Porcentagem é o valor obtido ao aplicarmos uma taxa percentual a um determinado valor.
|
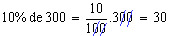
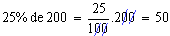 Logo, 50kg é o valor correspondente à porcentagem procurada.
Logo, 50kg é o valor correspondente à porcentagem procurada.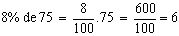
| r = an - an - 1 |
| ou seja |
| r = a2 - a1 = a3 - a2 = a4 - a3 = an - an-1 |
| an = an - 1 + r |
| ou seja |
| a2 = a1 + r |
| r = a2 - a1 | onde | a1 = 3 |
| r = 6 - 3 | a2 = 6 (a2 = a1 + r → a2 = 3 + 3 → a2 = 6) | |
| r = 3 | a3 = 9 (a3 = a1 + 2r → a3 = 3 + 2(3) → a3 = 3 + 6 → a3 = 9) |
| r = a2 - a1 | onde | a1 = 15 |
| r = 12 - 15 | a2 = 12 (a2 = a1 + r → a2 = 15 - 3 → a2 = 12) | |
| r = - 3 | a3 = 9 (a3 = a1 + 2r → a3 = 15 + 2(- 3) → a3 = 15 - 6 → a3 = 9) |
| r = a2 - a1 | onde | a1 = 6 |
| r = 6 - 6 | a2 = 6 (a2 = a1 + r → a2 = 6 + 0 → a2 = 6) | |
| r = 0 | a3 = 6 (a3 = a1 + 2r → a3 = 6 + 2(0) → a3 = 6 + 0 → a3 = 6) |
| Quadro Geral |
| P.A. crescente → r > 0 |
| P.A. decrescente → r < 0 |
| P.A. constante → r = 0 |
| a3 = (a2 + a4) / 2 → a3 = (8 + 14) / 2 → a3 = 22 / 2 → a3 = 11 |
| ou |
| a5 = (a4 + a6) / 2 → a5 = (14 + 20) / 2 → a5 = 34 / 2 → a5 = 17 |
| assim |
| an = [(an - 1) + (an + 1)] / 2 |
| a1 + a6 = 5 + 30 = 35 | ou seja | (a, b, c, d, e, f) |
| a2 + a5 = 10 + 25 = 35 | a + f = b + e = c + d | |
| a3 + a4 = 12 + 20 = 35 |
| a4 = (a2 + a6) / 2 a4 = (5 + 21) / 2 a4 = 26 / 2 a4 = 13 | a4 = (a3 + a5) / 2 a4 = (9 + 17) / 2 a4 = 26 / 2 a4 = 13 |
| Sn = [(ak + an) . n] / 2 | Sn → é o valor da soma dos termos da sequência ak → é o primeiro termo escolhido da sequência an → é o último termo escolhido da sequência n → é a posição do último termo escolhido da sequência |
| r = a3 - a2 r = 11 - 7 r = 4 | Ache o primeiro termo: a7 = a1 + 6r a7 = 3 + 6(4) a7 = 27 | Sn = [(ak + an) . n] / 2 Sn = [(3 + 27) . 7] / 2 Sn = [30 . 7] / 2 Sn = 210 / 2 Sn = 105 |
| an = ak + (n - k) . r 17 = 5 + (7 - 1) . r 17 = 5 + 6r 6r = 17 - 5 6r = 12 r = 2 | assim | (a1, a2, a3, a4, a5, a6, a7) → ( 5, 7, 9, 11, 13, 15, 17) |